Water collapse (explicit)

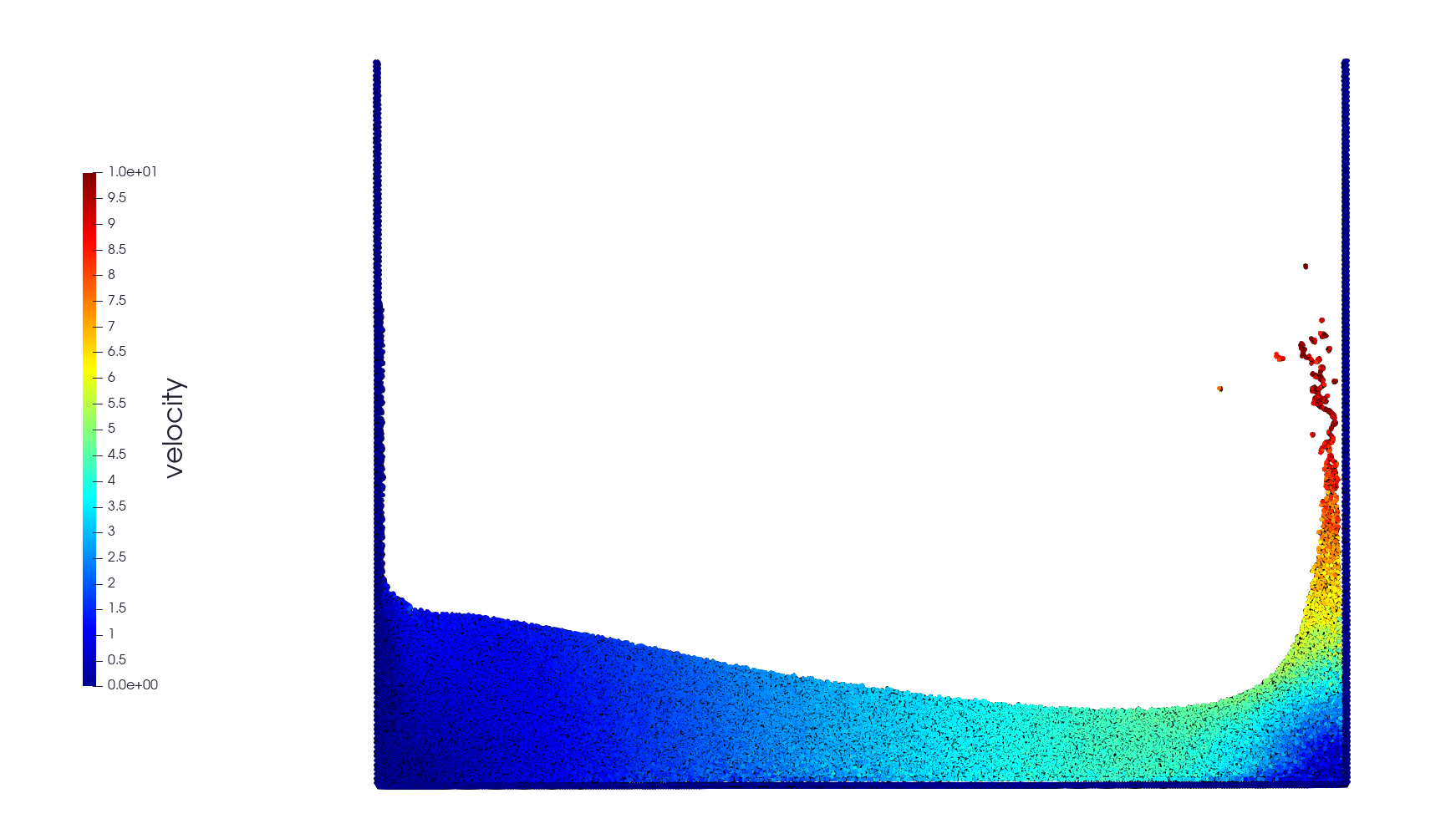
Simulation of a water column collapsing under its own weight. This would be very difficult to make in a mesh-based method like FDM, FEM or FVM. Fortunately, SPH turns this into an easy task. We use a very basic explicit SPH scheme with pressure-stabilized Verlet time integrator. This benchmark is (more or less) a recomputation of a simulation described in D. Violeau, FLUID MECHANICS AND THE SPH METHOD, page 484. We show how to implement it using SmoothedParticles.jl. Dependencies can be installed with

import Pkg
Pkg.add("Printf")
Pkg.add("CSV")
Pkg.add("DataFrames")
Pkg.add("Parameters")
Pkg.add("Plots")

Import essential packages.

module collapse_dry

using Printf
using SmoothedParticles
using CSV
using DataFrames
using Parameters
using Plots

Constant parameters

Importantly, modifier const avoids memory allocations.

# physical
const dr = 1.5e-2          # average particle distance (decrease to refine, increase to speed up)
const h = 3.0*dr           # size of kernel radius (twice the smoothing length)
const rho0 = 1000.   	   # fluid density
const m = rho0*dr^2        # particle mass
const c = 50.0             # numerical speed of sound
const g = -7.0*VECY        # gravitational acceleration
const mu = 8.4e-4          # dynamic viscosity of water
const nu = 1.0e-6          # artificial pressure stabilization

# geometrical
const water_column_width = 1.0
const water_column_height = 2.0
const box_height = 3.0
const box_width = 4.0
const wall_width = 2.5*dr

# temporal
const dt = 0.1*h/c                      # numerical time step
const t_end = 4.0                       # when to terminate (in seconds)
const dt_frame = max(dt,t_end/200)      # time step in the output (dt = dt_frame would save every frame, generating huge files)


##particle types
const FLUID = 0.   # fluid marker
const WALL = 1.    # wall marker

Particle variables

@with_kw mutable struct Particle <: AbstractParticle
	x::RealVector         # position
	v::RealVector = VEC0  # velocity
	Dv::RealVector = VEC0 # acceleration
	rho::Float64 = rho0   # density
	Drho::Float64 = 0.    # rate of density
	P::Float64 = 0.       # pressure
	type::Float64         # particle_type
end

Geometry

function make_system()
	grid = Grid(dr, :hexagonal)                                              # use hexagonal grid
	box = Rectangle(0., 0., box_width, box_height)                           # laboratory box
	fluid = Rectangle(0., 0., water_column_width, water_column_height)       # column of fluid
	walls = BoundaryLayer(box, grid, wall_width)                             # walls around laboratory box
	walls = Specification(walls, x -> (x[2] < box_height))                   # remove top lid
	sys = ParticleSystem(Particle, box + walls, h)                           # define particle system by specifying particle type, domain and maximal kernel radius
	generate_particles!(sys, grid, fluid, x -> Particle(x=x, type=FLUID))    # fill fluid geometry with particles
	generate_particles!(sys, grid, walls, x -> Particle(x=x, type=WALL))     # fill wall geometry with particles
	for p in sys.particles
		p.P = rho0*g[2]*(p.x[2] - water_column_height)                       # hydrostatic pressure
		p.rho = rho0 + p.P/c^2                                               # solve for density
	end
	return sys
end

Particle interactions

Rate of density is

$\dot{\varrho}_p = \sum_q m_q \left( \mathbf{x}_{pq} \cdot \mathbf{v}_{pq} + 2 \nu \varrho_{pq} \right) \frac{w'_{pq}}{r_{pq}}$

function balance_of_mass!(p::Particle, q::Particle, r::Float64)
	ker = m*rDwendland2(h,r)
	p.Drho += ker*(dot(p.x-q.x, p.v-q.v) + 2*nu*(p.rho-q.rho))
end

Linear formula for pressure. Tait equation can be used instead but the difference is mostly negligible.

$P_p = c^2 (\varrho_p - \varrho_0)$

function find_pressure!(p::Particle)
	p.rho += p.Drho*dt
	p.Drho = 0.0
	p.P = c^2*(p.rho - rho0)
end

Internal forces between particles are pressure and viscosity. Wall particles are excluded.

$\dot{\mathbf{v}}_p = -\sum_q m_q \left( \frac{P_p}{\rho_p^2} + \frac{P_q}{\rho_q^2} \right) \frac{w'_{pq}}{r_{pq}} \mathbf{x}_{pq} + \frac{2 \mu}{\rho_0^2}\sum_q m_q \frac{w'_{pq}}{r_{pq}} \mathbf{v}_{pq}$

function internal_force!(p::Particle, q::Particle, r::Float64)
	if p.type == FLUID
		ker = m*rDwendland2(h,r)
		p.Dv += -ker*(p.P/p.rho^2 + q.P/q.rho^2)*(p.x - q.x)
		p.Dv += +2*ker*mu/rho0^2*(p.v - q.v)
	end
end

Position and velocity updates

Updating by half-time step is a feature of Verlet integrator.

function move!(p::Particle)
	p.Dv = VEC0
	if p.type == FLUID
		p.x += 0.5*dt*p.v
	end
end

function accelerate!(p::Particle)
	if p.type == FLUID
		p.v += 0.5*dt*(p.Dv + g)
	end
end

Extract global variables

Variables of interest are total energy, water column height and wavefront location.

function energy(p::Particle)::Float64
	kinetic = 0.5*m*dot(p.v, p.v)
	potential = -m*dot(g, p.x)
	internal =  m*c^2*(log(abs(p.rho/rho0)) + rho0/p.rho - 1.0)
	return kinetic + potential + internal
end

function get_globals(sys::ParticleSystem)::NTuple{3,Float64}
	H = 0.0  # height of water column
	X = 0.0  # wavefront x-coordinate
	E = 0.0  # total energy
	for p in sys.particles
		if p.type == FLUID
			X = max(X, p.x[1]/water_column_width)
		end
		if p.type == FLUID && 2.0 > p.x[1] > h
			H = max(H, p.x[2]/water_column_height)
		end
		E += energy(p)
	end
	return (X,H,E)
end

Time loop

SmoothedParticles.jl will automatically run this in parallel and use neighbor list acceleration. Command create_cell_list!(sys) must be called at the beginning and each time after particles move.

function main()
	ts = []
	Xs = []
	Hs = []
	sys = make_system()
	out = new_pvd_file("results/collapse_dry")
	create_cell_list!(sys)
	apply!(sys, internal_force!)
	@time for k = 0 : round(Int64, t_end/dt)
		apply!(sys, accelerate!)
		apply!(sys, move!)
		create_cell_list!(sys)
		apply!(sys, balance_of_mass!)
		apply!(sys, find_pressure!)
		apply!(sys, move!)
		create_cell_list!(sys)
		apply!(sys, internal_force!)
		apply!(sys, accelerate!)
		# save data at selected frames
		if (k % round(Int64, dt_frame/dt) == 0)
			@printf("t = %.6e s ", k*dt)
			println("(",round(100*k*dt/t_end),"% complete)")
			(X, H, E) = get_globals(sys)
			@printf("energy = %.6e J\n", E)
			@printf("\n")
			push!(Xs, X)
			push!(Hs, H)
			push!(ts, k*dt*sqrt(-2*g[2]))
			save_frame!(out, sys, :v, :P, :type)
		end
	end
	save_pvd_file(out)
	data = DataFrame(time = ts, X = Xs, H = Hs)
	CSV.write("results/collapse_dry/data.csv", data)
	@info "drawing a plot with results"
	make_plot()
end ## function main

Compare computed results to the book by Violeau and the experiment of Koshizuka and Oka (1996)

function make_plot()
	data = CSV.read("results/collapse_dry/data.csv", DataFrame)
	X_VIO = CSV.read("reference/dambreak_X_Violeau.csv", DataFrame)
	X_KOS = CSV.read("reference/dambreak_X_Koshizuka.csv", DataFrame)
	H_VIO = CSV.read("reference/dambreak_H_Violeau.csv", DataFrame)
	H_KOS = CSV.read("reference/dambreak_H_Koshizuka.csv", DataFrame)
	p1 = plot(data.time, data.X, label = "SmoothedParticles.jl", xlims = (0., 3.0))
	scatter!(p1, X_VIO.time, X_VIO.X, label = "Violeau")
	scatter!(p1, X_KOS.time, X_KOS.X, label = "Koshizuka&Oda", markershape = :square)
	savefig(p1, "results/collapse_dry/dambreak_X.pdf")
	p2 = plot(data.time, data.H, label = "SmoothedParticles.jl", xlims = (0., 3.0))
	scatter!(p2, H_VIO.time, H_VIO.H, label = "Violeau")
	scatter!(p2, H_KOS.time, H_KOS.H, label = "Koshizuka&Oda", markershape = :square)
	savefig(p2, "results/collapse_dry/dambreak_H.pdf")
end

end ## module

This page was generated using Literate.jl.