Symplecticity & reversibility

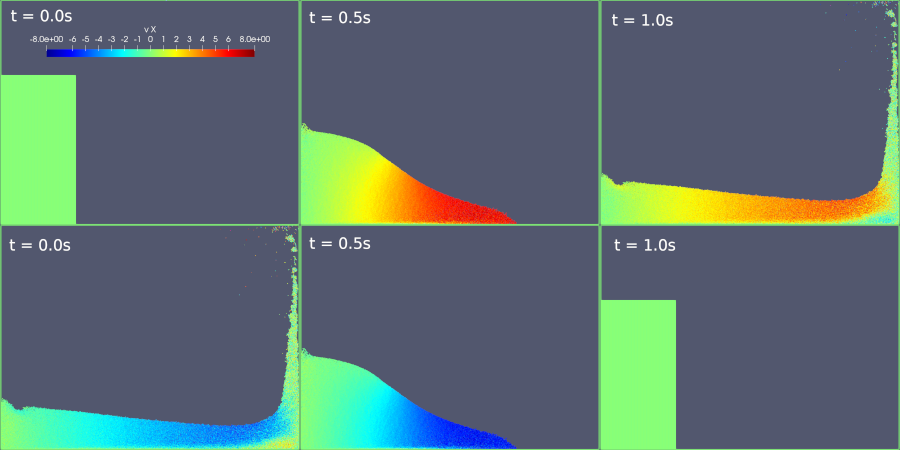
Simulation of a water column collapsing under its own weight onto dry bottom. Here we use a symplectic scheme and get a reversible simulation. At the end of the simulation, the velocities are reverted and the simulation goes back to its initial conditions. Despite the reversibility, Boltzmann entropy grows and attains its maximum value just before the velocities are reverted.

module collapse_symplectic

using Printf
using SmoothedParticles
using Parameters
using Plots
using DataFrames # to store the csv file
using CSV# to store the csv file
include("utils/FixPA.jl")
include("utils/entropy.jl")
using .FixPA
using .entropy


#using ReadVTK  #not implemented
#using VTKDataIO

Declare constant parameters

##physical
const dr = 1.0e-2          # average particle distance (decrease to refine, increase to speed up)
const h = 3.0*dr           # kernel radius
const rho0 = 1000.   	   # fluid density
const m = rho0*dr^2        # particle mass
const g = -9.8*VECY        # gravitational acceleration
const mu = 0.0#8.4e-4      # dynamic viscosity of water

##geometrical
const water_column_width = 1.0
const water_column_height = 2.0
const box_height = 3.0
const box_width = 4.0
const wall_width = 2.5*dr


##artificial
const c = 50.0             #numerical speed of sound
const dr_wall = 0.95*dr
const E_wall = 10*norm(g)*water_column_height
const eps = 1e-16

##temporal
const dt = 0.1*h/c
const t_end = 1.0
const dt_frame = t_end/100

##particle types
const FLUID = 0.
const WALL = 1.

@with_kw mutable struct Particle <: AbstractParticle
	x::RealVector #position
	v::RealVector = VEC0 #velocity
	a::RealVector = VEC0 #acceleration
	P::Float64 = 0. #pressure
	rho::Float64 = 0. #density
    rho0::Float64 = 0.
	type::Float64 #particle_type
end

Define geometry and make particles

function make_system()
	grid = Grid(dr, :square)
	box = Rectangle(0., 0., box_width, box_height)
	fluid = Rectangle(0., 0., water_column_width, water_column_height)
	walls = BoundaryLayer(box, grid, wall_width)
	#walls = Specification(walls, x -> (x[2] < box_height))
	domain = Rectangle(-box_width, -box_width, 2*box_width, 3*box_height)
	sys = ParticleSystem(Particle, domain, h)
	generate_particles!(sys, grid, fluid, x -> Particle(x = x, type = FLUID))
	generate_particles!(sys, grid, walls, x -> Particle(x = x, type = WALL))
	return sys
end

Define particle interactions

@inbounds function find_rho!(p::Particle, q::Particle, r::Float64)
    if p.type == FLUID && q.type == FLUID
		p.rho += m*wendland2(h,r)
	end
end

@inbounds function find_rho0!(p::Particle, q::Particle, r::Float64)
    if p.type == FLUID && q.type == FLUID
		p.rho0 += m*wendland2(h,r)
	end
end

function find_pressure!(p::Particle)
	p.P = c^2*(p.rho - p.rho0)
end

@inbounds function internal_force!(p::Particle, q::Particle, r::Float64)
	if p.type == FLUID && q.type == FLUID
		ker = m*rDwendland2(h,r)
		p.a += -ker*(p.P/p.rho^2 + q.P/q.rho^2)*(p.x - q.x)
		#p.a += +2*ker*mu/rho0^2*(p.v - q.v)
	elseif p.type == FLUID && q.type == WALL && r < dr_wall
		s = dr_wall/(r + eps)
		p.a += -E_wall/(r + eps)^2*(s^2 - s^4)*(p.x - q.x)
	end
end

function reset_a!(p::Particle)
    p.a = zero(RealVector)
end

function reset_rho!(p::Particle)
    p.rho = 0.0
end

function move!(p::Particle)
	if p.type == FLUID
		p.x = rev_add(p.x, dt*p.v)
	end
end

function accelerate!(p::Particle)
	if p.type == FLUID
		p.v = rev_add(p.v, 0.5*dt*(p.a + g))
	end
end

function LJ_potential(p::Particle, q::Particle, r::Float64)::Float64
	if q.type == WALL && p.type == FLUID && r < dr_wall
		s = dr_wall/(r + eps)
		return m*E_wall*(0.5s^2 - 0.25s^4 -0.25)
	else
		return 0.0
	end
end

function energy_kinetic(sys::ParticleSystem)::Float64
	return sum(p -> 0.5*m*dot(p.v, p.v), sys.particles)
end

function energy(sys::ParticleSystem, p::Particle)::Float64
	kinetic = 0.5*m*dot(p.v, p.v)
	internal =  m*c^2*(rho0/p.rho + log(abs(p.rho0/rho0)) - 2.0)
	gravity_potential = -m*dot(g, p.x)
	wall_potential = SmoothedParticles.sum(sys, LJ_potential, p)
	return kinetic + internal + gravity_potential + wall_potential
end

Put everything into a time loop

function verlet_step!(sys::ParticleSystem)
    apply!(sys, accelerate!)
    apply!(sys, move!)
    create_cell_list!(sys)
    apply!(sys, reset_rho!)
    apply!(sys, find_rho!, self = true)
    apply!(sys, find_pressure!)
    apply!(sys, reset_a!)
    apply!(sys, internal_force!)
    apply!(sys, accelerate!)
end

function save_results!(out::SmoothedParticles.DataStorage, sys::ParticleSystem, k::Int64)
    if (k %  Int64(round(dt_frame/dt)) == 0)
        @printf("t = %.6e\n", k*dt)
        #energy
        E = sum(p -> energy(sys,p), sys.particles)
        @show E
        println("# of part. = ", length(sys.particles))
        println()
        save_frame!(out, sys, :v, :a, :P, :rho, :rho0)
    end
end

function main(;revert = true) #if revert=true, velocities are inverted at the end of the simulation and the simulation then goes backward
	sys = make_system()
	out = new_pvd_file("results/collapse_fixpa")
    #initialization
    create_cell_list!(sys)
    apply!(sys, find_rho0!, self = true)
    apply!(sys, find_rho!, self = true)
    apply!(sys, find_pressure!)
    apply!(sys, internal_force!)

	N_of_particles = length(sys.particles)
	@show(N_of_particles)
	@show(m)


	step_final = Int64(round(t_end/dt))
	times = Float64[] #time instants
	Ss = Float64[] # Entropy values
	Ekin = Float64[] # Kinetic energy values
	for k = 0 : step_final
        verlet_step!(sys)
        save_results!(out, sys, k)
    	if k % round(step_final/100) == 0 # store a number of entropy values
			distr = velocity_histogram(sys, N = 100)
			S = entropy_2D_MB(distr)
			push!(times, k*dt)
			push!(Ss, S)
			push!(Ekin, energy_kinetic(sys))
			@show(S)
        	println()
		end
	end

Plotting the velocity distribution in comparison with Maxwell-Boltzmann

	T = plot_velocity_distr(sys, m, "energy_distribution_middle.pdf")

Plotting the entropy in time

	Sred_eq_E = [(1+log(Ekin[k]/(m*length(sys.particles)))) for k in 1:length(Ss)]
	Sred_eq_T= (1+log(kB*T/m))*ones(Float64, length(Ss))
	p = plot(times, [Ss Sred_eq_T Sred_eq_E], label = ["entropy" "S_eq(T)" "S_eq(E)"],legend=:bottomright)
	savefig(p, "entropy_middle.pdf")
	df = DataFrame(time_steps = times, S_Boltzmann = Ss, S_eq_T = Sred_eq_T, S_eq_E = Sred_eq_E)
	CSV.write("entropy_middle.csv", df)

	if revert
		#revert velocities
		println("--------------------")
		println("Reverting velocities")
		println("--------------------")
		for p in sys.particles
			p.v = -p.v
		end
		Ss_rev = Float64[]
		for k = step_final:-1:0
			verlet_step!(sys)
			save_results!(out, sys, k)
			if k % round(step_final/100) == 0 # store a number of entropy values
				distr = velocity_histogram(sys, v_max = sqrt(2*norm(g)*water_column_height), N = 100)
				S = entropy_2D_MB(distr)
				push!(Ss_rev, S)
				@show(S)
				println()
			end
		end
		plot_velocity_distr(sys, m, "energy_distribution_final.pdf")

Plotting the entropy in time

		p = plot(times, [Ss Ss_rev Sred_eq_T Sred_eq_E], label = ["entropy forward" "entropy backward" "S_eq(T)" "S_eq(E)"], legend=:bottomright)
		savefig(p, "entropy_final.pdf")
		df = DataFrame(time_steps = times, S_Boltzmann = Ss, S_eq_T = Sred_eq_T, S_eq_E = Sred_eq_E)
		CSV.write("entropy_final.csv", df)
	end

	save_pvd_file(out)

end ## function main

end ## module

This page was generated using Literate.jl.