Water collapse (implicit)

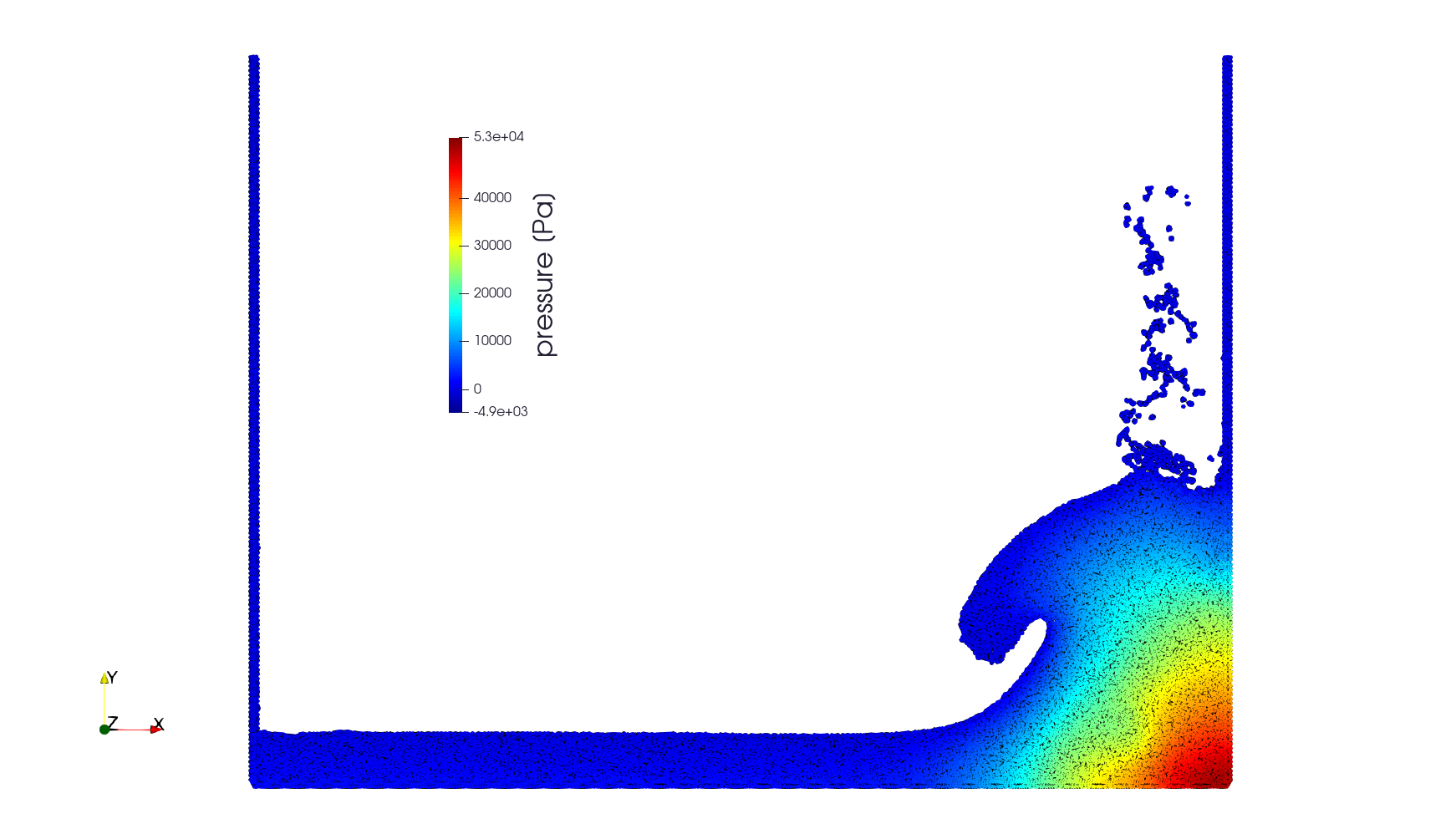
Simulation of a water column, this time using incompressible SPH. This works by first applying all non-pressure forces to find intermeidate velocity $\mathbf{v}^*$. The pressure-corrected velocity

$\mathbf{v} = \mathbf{v}^* - \frac{\delta t}{\varrho} \nabla P$

is found such that $\mathbf{v}$ is a divergence-free vector field. Taking divergence of both sides leads to a poisson problem

$- \Delta P = -\frac{\varrho}{\delta t} \nabla \cdot \mathbf{v}^*.$

A homogeneous Dirichlet condition for pressure is prescribed at the boundary. Free surface can be identified using a trick invented by Lee (2008). A parameter is defined

$\lambda = 1 - \frac{1}{d} \nabla \cdot {\mathbf{r}}$

which is zero inside the fluid but positive on the boundary. Boundary condition can be implemented smoothly by adding a penalty term:

$- \Delta P + C_\mathrm{free} \lambda P = -\frac{\varrho}{\delta t} \nabla \cdot \mathbf{v}^*.$

To get a particle approximation, we replace $\Delta$ with a Morris operator and $\nabla \cdot$ with the usual divergence operator. This yields a system with a positive definite matrix.

module collapse_dry_implicit

using Printf
using SmoothedParticles
using CSV
using DataFrames
using LinearAlgebra
using IterativeSolvers
using IncompleteLU
using Parameters
using Plots

Constant parameters

##kernel functions
const kernel = spline23
const Dkernel = Dspline23
const rDkernel = rDspline23

const dim = 2
const dr = 1.0e-2         # average particle distance (decrease to refine, increase to speed up)
const h = 2.8*dr          # size of kernel support
const rho = 1000.0        # fluid density
const g = -9.8*VECY       # gravitational acceleration
const mu = 8.4e-4         # dynamic viscosity
const m = dr^dim*rho      # particle mass
const C_free = 10.0       # free surface penalty coefficient
const v_char = 5.0        # char velocity

##geometry parameters
const water_column_width = 1.0
const water_column_height = 2.0
const box_height = 3.0
const box_width = 4.0
const nlayers = 3.5
const wall_width = nlayers*dr

##temporal parameters
const dt = 0.1*h/v_char
const t_end = 2.0
const dt_frame = max(dt, t_end/200)

##labels for particle types
const FLUID = 0.
const  WALL = 1.
const DUMMY = 2.

Particle variables

@with_kw mutable struct Particle <: AbstractParticle
	x::RealVector = VEC0   #position
	v::RealVector = VEC0   #velocity
	Dv::RealVector = VEC0  #acceleration
	P::Float64 = 0.0       #pressure
	div::Float64 = 0.0     #divergence of velocity
	L::Float64 = 0.0       #diagonal element of projection matrix
	lambda::Float64 = 0.0  #free surface indetifier
	type::Float64          #particle type
end

Geometry

function make_system()
	grid = Grid(dr, :hexagonal)
	box = Rectangle(0., 0., box_width, box_height)
	fluid = Rectangle(0., 0., water_column_width, water_column_height)
	walls = Specification(BoundaryLayer(box, grid, 1.2*dr), x -> (x[2] < box_height))
	dummy = Specification(BoundaryLayer(box, grid, nlayers*dr) - walls, x -> (x[2] < box_height))
	sys = ParticleSystem(Particle, fluid + dummy + walls, h)
	generate_particles!(sys, grid, fluid, x -> Particle(x=x, type=FLUID))
	generate_particles!(sys, grid, walls, x -> Particle(x=x, type=WALL))
	generate_particles!(sys, grid, dummy, x -> Particle(x=x, type=DUMMY))
	create_cell_list!(sys)
	return sys
end

Particle interactions

function initialize!(p::Particle)
	if p.type == FLUID
		p.x += dt*p.v
		p.v += dt*g
	end
	p.div = 0.0
	p.L = 0.0
	p.lambda = 1.0
end

function viscous_force!(p::Particle, q::Particle, r::Float64)
	p.Dv += 2.0*m*mu*rDkernel(h,r)/rho^2*(p.v - q.v)
end

function internal_force!(p::Particle, q::Particle, r::Float64)
	p.Dv -= m*rDkernel(h,r)*(p.P + q.P)/rho^2*(p.x - q.x)
end

function accelerate!(p::Particle)
	if p.type == FLUID
		p.v += dt*p.Dv
	end
	p.Dv = VEC0
end

Functions to build the linear system

function div_L_lambda!(p::Particle, q::Particle, r::Float64)
	rDk = rDkernel(h,r)
	p.div += -SmoothedParticles.dot(p.x - q.x, p.v - q.v)*m*rDk
	p.L += -2.0*m/rho*rDk
	p.lambda += m/rho*rDk*r^2/dim
end

function projection_matrix(p::Particle, q::Particle, r::Float64)::Float64
	if p == q
		if p.type == FLUID
			return h^2*p.L + C_free*max(p.lambda, 0.)
		else
			return h^2*p.L
		end
	end
	return 2.0*h^2*m/rho*rDkernel(h,r)
end

function projection_vector(p::Particle)::Float64
	return -h^2*p.div/dt
end

Extract global variables

Variables of interest are total energy, water column height and wavefront location.

function energy(p::Particle)::Float64
	kinetic = 0.5*m*SmoothedParticles.dot(p.v, p.v)
	potential = -m*SmoothedParticles.dot(g, p.x)
	return kinetic + potential
end

function get_globals(sys::ParticleSystem)::NTuple{3,Float64}
	H = 0.0  # height of water column
	X = 0.0  # wavefront x-coordinate
	E = 0.0  # total energy
	for p in sys.particles
		if p.type == FLUID
			X = max(X, p.x[1]/water_column_width)
		end
		if p.type == FLUID && 2.0 > p.x[1] > h
			H = max(H, p.x[2]/water_column_height)
		end
		E += energy(p)
	end
	return (X,H,E)
end

Time iteration

function main()
	sys = make_system()
	out = new_pvd_file("results/collapse_dry_implicit")
	P = ParticleField(sys, :P)
	ts = []
	Xs = []
	Hs = []
	@time for k = 0 : Int64(round(t_end/dt))
		if (k %  Int64(round(dt_frame/dt)) == 0)
			@printf("t = %.6e s ", k*dt)
			println("(",round(100*k*dt/t_end),"% complete)")
			(X, H, E) = get_globals(sys)
			@printf("energy = %.6e J\n", E)
			@printf("\n")
			push!(Xs, X)
			push!(Hs, H)
			push!(ts, k*dt*sqrt(-2*g[2]))
			save_frame!(out, sys, :v, :P, :type)
		end
		apply!(sys, initialize!)
		create_cell_list!(sys)
		apply!(sys, viscous_force!)
		##assemble linear system and solve for pressure
		apply!(sys, div_L_lambda!)
		A = assemble_matrix(sys, projection_matrix)
		b = assemble_vector(sys, projection_vector)
		try
			#P .= A\b
			P .= cg(A, b)#; Pl = ilu(A; τ = 0.1))
		catch
			save_pvd_file(out)
			error("Unable to solve linear system.")
		end
		apply!(sys, internal_force!)
		apply!(sys, accelerate!)
	end
	save_pvd_file(out)
	data = DataFrame(time = ts, X = Xs, H = Hs)
	CSV.write("results/collapse_dry_implicit/data.csv", data)
	@info "drawing a plot with results"
	make_plot()
end

Compare computed results to the book by Violeau.

function make_plot()
	data = CSV.read("results/collapse_dry_implicit/data.csv", DataFrame)
	X_VIO = CSV.read("reference/dambreak_X_Violeau.csv", DataFrame)
	X_KOS = CSV.read("reference/dambreak_X_Koshizuka.csv", DataFrame)
	H_VIO = CSV.read("reference/dambreak_H_Violeau.csv", DataFrame)
	H_KOS = CSV.read("reference/dambreak_H_Koshizuka.csv", DataFrame)
	p1 = plot(data.time, data.X, label = "SmoothedParticles.jl", xlims = (0., 3.0))
	scatter!(p1, X_VIO.time, X_VIO.X, label = "Violeau")
	scatter!(p1, X_KOS.time, X_KOS.X, label = "Koshizuka&Oda", markershape = :square)
	savefig(p1, "results/collapse_dry_implicit/dambreak_X.pdf")
	p2 = plot(data.time, data.H, label = "SmoothedParticles.jl", xlims = (0., 3.0))
	scatter!(p2, H_VIO.time, H_VIO.H, label = "Violeau")
	scatter!(p2, H_KOS.time, H_KOS.H, label = "Koshizuka&Oda", markershape = :square)
	savefig(p2, "results/collapse_dry_implicit/dambreak_H.pdf")
end

end

This page was generated using Literate.jl.