Example 6: Triple-point problem

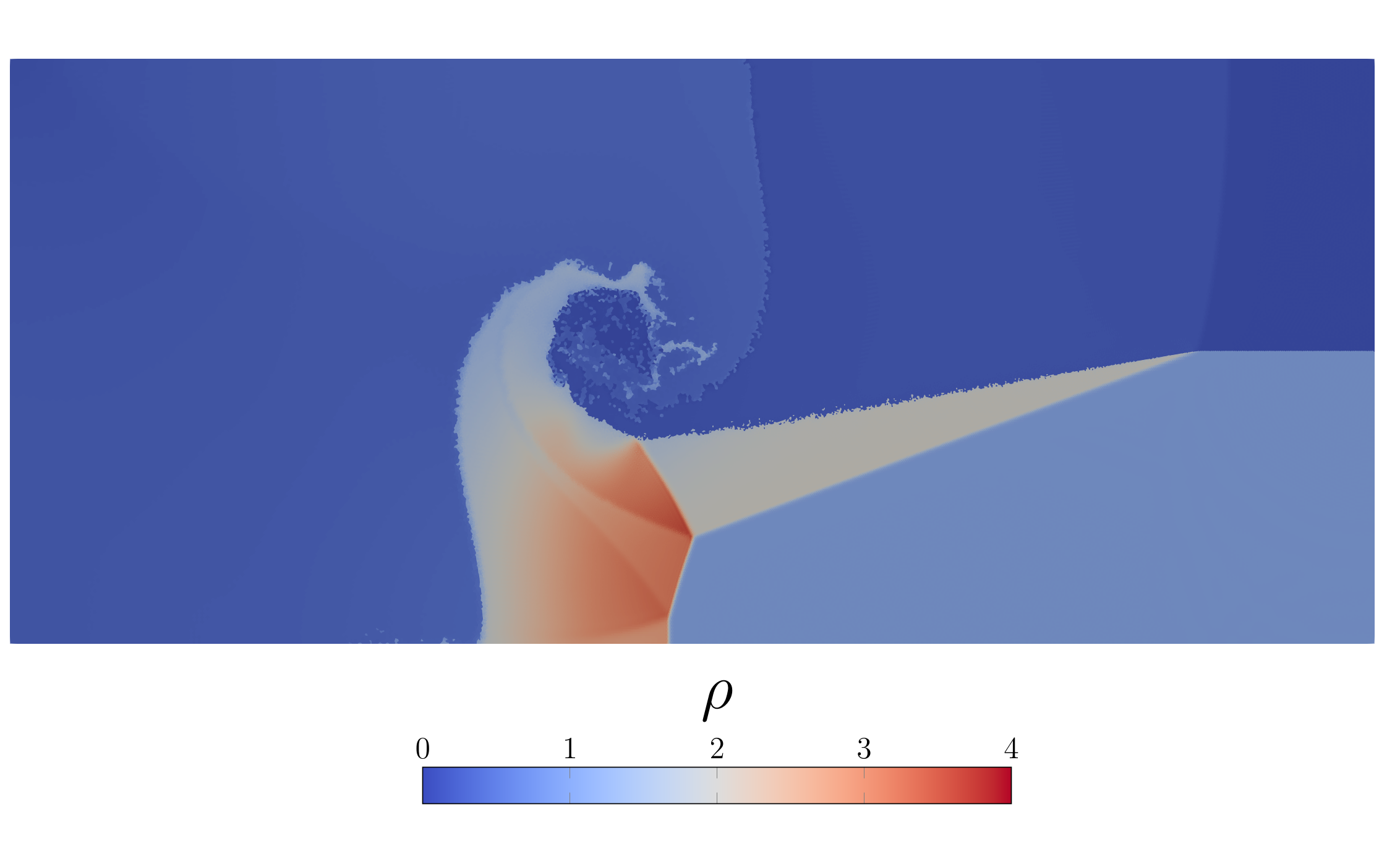
Triple point is a fancy benchmark which contains three separate gases with different properties. It is described in detail in this paper and is essentially a two-dimensional version of a Riemann Problem. Scientists like it just because it creates a very cool spiral.

module triplepoint

include("../src/LagrangianVoronoi.jl")
using .LagrangianVoronoi, Polyester


const rho0 = 1.0
const xlims = (0.0, 7.0)
const ylims = (0.0, 3.0)
const dr = 1e-2
const nframes = 200
const CFL = 0.1
const v_char = 1.5
const dt = CFL*dr/v_char
const t_end = 3.0
const export_path = "results/triplepoint"

This struct helps to reduce the number of constant variables. Numbers xmin, xmax, ymin, ymax specify the rectangle where the phase is located at t = 0.

struct FluidPhase
    label::Int      # phase label
    rho::Float64    # initial density
    P::Float64      # initial density
    gamma::Float64  # adiabatic index
    xmin::Float64
    xmax::Float64
    ymin::Float64
    ymax::Float64
end
const phase1 = FluidPhase(1, 1, 1, 1.5, 0, 1, 0, 3)
const phase2 = FluidPhase(2, 1, 0.1, 1.4, 1, 7, 0, 1.5)
const phase3 = FluidPhase(3, 0.125, 0.1, 1.5, 1, 7, 1.5, 3)
const fluidphases = [phase1, phase2, phase3]

function ic!(p::VoronoiPolygon)
    for fp in fluidphases
        if (fp.xmin <= p.x[1] <= fp.xmax) && (fp.ymin <= p.x[2] <= fp.ymax)
            p.phase = fp.label
            p.rho = fp.rho
            p.P = fp.P
            p.e = p.P/(p.rho*(fp.gamma - 1.0))
            p.mass = p.rho*area(p)
        end
    end
end

Let us define our custom equation of state, which is different for every fluid phase. The @batch macro from the Polyester package makes it run in parallel. It is approximately godzillion times faster than @threads.

function multi_eos!(grid::VoronoiGrid)
    @batch for p in grid.polygons
        fp = fluidphases[p.phase]
        p.rho = p.mass/area(p)
        eps = p.e - 0.5*norm_squared(p.v)
        p.P = (fp.gamma - 1.0)*p.rho*eps
        p.c2 = fp.gamma*p.P/p.rho
        if p.P <= 0.0
            throw("there was a negative pressure")
        end
    end
end

The rest of the script is just the standard procedure.

mutable struct Simulation <: SimulationWorkspace
    grid::GridNS
    psolver::PressureSolver
    msolver::MultiphaseSolver
    E::Float64
    S::Float64
    E0::Float64
    S0::Float64
    quality::Float64
    first_step::Bool
    Simulation() = begin
        domain = Rectangle(xlims = xlims, ylims = ylims)
        grid = GridNS(domain, dr)
        populate_hex!(grid, ic! = ic!)
        psolver = PressureSolver(grid)
        msolver = MultiphaseSolver(grid)
    return new(grid, psolver, msolver, 0.0, 0.0, 0.0, 0.0, 0.0, true)
    end
end

function step!(sim::Simulation, t::Float64)
    move!(sim.grid, dt)
    multi_eos!(sim.grid)
    find_pressure!(sim.psolver, dt)
    pressure_step!(sim.grid, dt)
    find_D!(sim.grid)
    viscous_step!(sim.grid, dt)
    find_dv!(sim.grid, dt)
    multiphase_projection!(sim.msolver)
    relaxation_step!(sim.grid, dt)
    return
end


function postproc!(sim::Simulation, t::Float64)
    @show t
    grid = sim.grid
    sim.E = 0.0
    sim.S = 0.0
    sim.quality = Inf
    for p in grid.polygons
        fp = fluidphases[p.phase]
        sim.E += p.mass*p.e
        sim.S += p.mass*(log(abs(p.P)) - fp.gamma*log(abs(p.rho)))
        sim.quality = min(sim.quality, p.quality)
    end
    if sim.first_step
        sim.E0 = sim.E
        sim.S0 = sim.S
        sim.first_step = false
    end
    sim.E -= sim.E0
    sim.S -= sim.S0
    @show sim.E
    @show sim.S
    @show sim.quality
    println()
    return
end

function main()
    sim = Simulation()
    run!(sim, dt, t_end, step!;
        postproc! = postproc!,
        nframes = nframes,
        path = export_path,
        save_csv = false,
        save_points = true,
        save_grid = true,
        vtp_vars = (:P, :v, :rho, :phase, :quality)
    )
end

if abspath(PROGRAM_FILE) == @__FILE__
    main()
end

end

This page was generated using Literate.jl.